シグモイド関数を理解しようと思ったら、対数も勉強する必要があった。もうやけくそです。高校時代にしっかり数学勉強しておけばよかった。。。。
参考
唯一の救いは、上記のような素晴らしいページがあったこと。大変参考にさせて頂きました。有難うございます。
本ページは、自分の理解向上のため、上記URL記載内容を自分の言葉で書いたものです。対数を学びたい人は、上記URLを見た方がいいです。
指数と対数とは?
・指数は、2^3 = 8の3の部分
対数表記だと3 = log2(8)
・指数と同じものを意味するもの。
※指数の別表記
・キーワード
【指数表記の場合】
x = a^p
pは指数(冪指数)
【対数表記の場合】
p = loga(x)
loga(x)は対数(指数pと同じもの。表記によって呼び方が変わる)
aは底(base)
xは進数
式の意味は、aを何乗したらxになるか?答えはp
★指数の加減算は、真数に対する乗除算になる。これが重要なポイント★
累乗根とは?
・rootと呼ばれる
指数と逆の計算をするもの
・キーワード
累乗(冪乗) = 指数
累乗根(冪乗根) = 底
・数式は以下の通り
2乗したら4になる数値は何か?
√4 = 2
以下表記も可能
2√4 = 2
※√の前の2は小字
3乗したら8になる数値は何か?
3√8 = 2
※√の前の3は小字
・平方根/立方根も累乗根の一部
2乗根は平方根、3乗根は立方根と呼ばれる。
指数の拡張とは?
log2(4)=2
上記は簡単。指数が整数で表わせる為。
だけど以下はどうか?
log2(5)
指数の拡張の考えで上記は算出できる。
指数の拡張とは、指数を整数以外で表すこと
※これが大発見であった!
指数の拡張は以下の通り
①ゼロの指数
a^0 = 1
指数が一つあがると、底の掛け算が発生する。
指数が一つ下がると、底の割り算が発生する。
この関係性でいくと、2^0は1になる。
純粋に直感で0乗=1もしっくりくる。
②マイナスの指数
1
a^(-p) = -----
a^p③分数/少数の指数
以下の定義があり。
a^(1/n) = n√a
※上記の√の前のnは小字
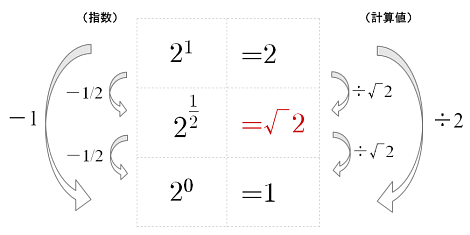
この定義を理解する為の図。(参考URLから引用)
例) 2^(1/2) = 2√2
※上記の√の前の2は小字
指数を減算する時は、除算が行われる。
※底が2の場合
指数が1減ったら2で除算される。
指数が1増えたら2で乗算される。
指数が1/2増えるとは、√2で乗算すること。
指数に対して1/2の加算を2回すると、1加算した場合と同じ効果を与える。
指数を1/2加算した場合は、√2が乗算される。もう一回指数を1/2すると、更に√2が乗算される。
→√2 * √2 = 2
→1加算した場合と同じ効果になる
a^(1/n) = n√a
上記は、aのn乗根ともいえる。
a^(0.5) = a^(1/2) = n√a
指数が少数である場合も、分数と同じ考えでOK
指数法則
①a^m * a^n = a^(m+n)
②a^m / a^n = a^(m-n)
③(a^m)^n = a^(m*n)
④(a*b)^m = a^m * b^m
指数法則 使用例
ゼロの指数
a^3 / a^3 = a^(3-3) = a^0 = 1
マイナスの指数
1
a^2 * a^(-4) = a^(2-4) = a^(-2) = -----
a^2分数の指数
(a^(1/3))^3 = a^(1/3 * 3) = a^1 = a (a^(1/3))^3 = (3√a)^3 = a
おまけ
(a^2)^(1/3) = a^(2*1/3) = a^(2/3) = 3√a^2 指数の分子が1以外の時は上記の計算が可能。 →aの2/3乗 = aの2乗の3乗根
対数公式
これ重要!
①loga(B*C) = loga(B) + loga(C)
証明
a^m = B a^n = C とすると B*C = a^m * a^n = a^(m+n) 上記はB*Cはaをm+n乗したものを意味する 上記を対数表記すると loga(B*C) = m + n 更にmとnを展開する mは前提であるa^m = Bより、m = loga(B) nも前提であるa^n = Cより、m = loga(C) よって、 loga(B*C) = loga(B) + loga(C)
②loga(B/C) = loga(B) - loga(C)
証明
B = a^m C = a^n とすると、 loga(B/C) = loga(a^m/a^n) = loga(a^(m-n)) = m-n mとnを展開すると、 = loga(B) - loga(C)
③loga(B^c) = c * loga(B)
★真数の指数は対数の外に出せる★
証明
B = a^m とすると。 loga(B^c) = loga((a^m)^c) = loga(a^(m*c)) = m*c mを展開すると、 = loga(B) * c
④logb(c) = loga(c)/loga(b)
証明
loga(c)
logb(c) = ---------
loga(b)
左辺をxとする。
loga(c)
x = ---------
loga(b)
両辺にloga(b)を掛ける
x * loga(b) = loga(c)
外のxを対数公式を適用して指数に戻す
loga(b^x) = loga(c)
底はどちらもa。そのため、上記式が成立するということは真数部分が同じ。
b^x = c
上記を以下に展開
x = logb(c)
上記xを最初に定義した以下式に代入すると
loga(c)
x = ---------
loga(b)
以下のように公式が証明される
loga(c)
logb(c) = ---------
loga(b)
aを10にすれば、任意の対数(logb(c))を常用対数に変換することができる!
⑤loga(b) * logb(a) = 1
★底と真数をひっくり返した対数同士を掛け合わせると1になる★
以下の公式も成り立つ
1
loga(b) = ---------
logb(a) 証明
底の返還を使う!
logc(b) logc(a)
loga(b) * logb(a) = ------- * ------- = 1
logc(a) logc(b)
鮮やかすぎる!
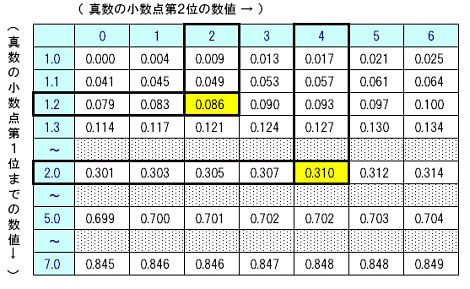
対数表とは?
※以下図は参考URLより引用
対数表は広く対応値を記載する必要はなしOK。
対数公式で展開して、整数に変換しきれない部分のみ対応表に記載されていれば結果を算出可能である為。
例) log200の場合
対数公式で展開
log200 = log10(200) = log10(2) + log10(100) = log10(2) + 2
→log10(2)が対応表に記載されていれば結果算出が可能。上記の対応表ではlog10(2)は真数部分が2の為、0.301。
例) log0.07の場合
対数公式で展開
log0.07 = log10(0.07) = log10(7/100) = log10(7) - log10(100) = log10(7) - 2